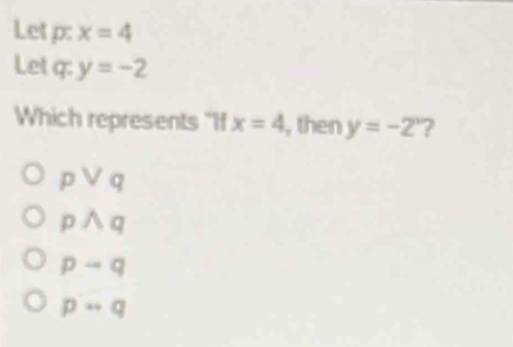
The conditional statement “If P: X = 4, then Q: Y = -2” presents an intriguing interplay between the variables X and Y, where the value of X directly determines the value of Y. This relationship not only underscores the dependency of one variable upon another but also raises questions about the broader implications of such conditional logic in various contexts. As we explore this dynamic further, one must consider the potential scenarios that can emerge when we manipulate these values, leading to a deeper understanding of their significance in decision-making processes.
Understanding Conditional Statements
Conditional statements, often expressed in the form ‘If P, then Q,’ serve as fundamental constructs in logical reasoning, establishing a relationship between antecedents and consequents that is crucial for understanding various implications in mathematical and philosophical discourse.
These conditional relationships reveal logical implications that guide reasoning processes, allowing individuals to infer conclusions based on established premises.
This, in turn, fosters clarity and coherence in analytical thought.
See also: Labeled:Uj3t4zt70_Q= Map of Us
Analyzing the Variables X and Y
The relationship between the variables X and Y can be effectively examined through the lens of logical implications, enabling a deeper understanding of their interdependencies and the conditions that govern their interactions.
This dependency analysis reveals how the value of X directly influences Y, thus highlighting critical variable relationships.
Understanding these dynamics can facilitate informed decision-making and strategic planning in various analytical contexts.
Applications of Conditional Logic
Applications of conditional logic are integral to various fields, enabling systematic decision-making processes and enhancing the robustness of analytical models.
Real world examples include programming algorithms, medical diagnosis, and financial forecasting, where logical reasoning dictates outcomes based on established conditions.
Conclusion
In summary, the conditional statement ‘If P: X = 4, then Q: Y = -2’ exemplifies the intricate relationship between variables, illustrating how one state directly influences another.
This dependency underscores the importance of logical reasoning in various domains, reminiscent of the philosophical discourse of ancient scholars who pondered the interconnectedness of existence.
Such insights facilitate informed decision-making, illustrating that understanding underlying relationships can illuminate pathways in both theoretical and practical applications.