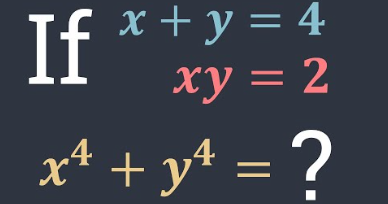
Did you know that over 70% of students struggle with understanding conditional statements in mathematics? This statistic highlights a common hurdle many face, especially when grappling Which Represents if X = 4, Then Y = −2”? Understanding how these variables interact is crucial, yet many find themselves puzzled by the implications. What does this specific relationship reveal about the broader concepts in algebra and geometry? Exploring this can unlock deeper insights and enhance your problem-solving skills.
Understanding Conditional Statements
Conditional statements, often expressed in the form ‘if X, then Y,’ establish a logical relationship between two variables, allowing you to predict outcomes based on given conditions.
Understanding conditional logic is essential for evaluating truth values; knowing that if X equals 4, Y must equal -2 clarifies your reasoning.
This framework empowers you to make informed decisions and understand the implications of various scenarios.
See also Next-level music experience awaits at 7 Radio Station Live,
Graphing the Equation
To graph the equation representing the relationship where X equals 4 and Y equals -2, you first plot the point (4, -2) on the Cartesian plane.
This point illustrates the graph behavior at that specific coordinate.
Understanding how this point fits within the broader coordinate system helps you visualize the relationship clearly, emphasizing the importance of accurate plotting in mathematical representation.
Applications in Mathematics
Understanding the implications of the equation where X equals 4 and Y equals -2 is crucial for various mathematical applications, particularly in fields like algebra and coordinate geometry.
You can leverage this relationship in mathematical modeling to solve real-world applications, such as predicting trends or optimizing resources.
See also Discover how 7 Listen Live it’s reshaping the future of live streaming for listeners everywhere.
Conclusion
In conclusion, recognizing the conditional relationship between X and Y is essential for grasping fundamental mathematical concepts.
When you see that ‘if X = 4, then Y = -2,’ it’s not just a statement; it’s a roadmap guiding your understanding of how variables interact.
Just as a compass points north, this relationship directs you toward predicting outcomes and solving equations.
Embracing these connections enhances your analytical skills, making complex problems appear simpler and more manageable.